
prefeitura MUNICIPAL DE IÚNA
ESTADO DO ESPÍRITO SANTO
LEI COMPLEMENTAR Nº 27, DE 28 DE DEZEMBRO DE 2021
|
INSTITUI A PLANTA GENÉRICA DE VALORES - PGV DO MUNICÍPIO DE IÚNA; ALTERA E ACRESCENTA DISPOSITIVOS NA LEI 1.989, DE 08 DE DEZEMBRO DE 2005 (CÓDIGO TRIBUTÁRIO MUNICIPAL). |
O PREFEITO MUNICIPAL DE IÚNA, ESTADO DO ESPÍRITO SANTO FAÇO SABER QUE A CÂMARA MUNICIPAL APROVOU E EU SANCIONO A SEGUINTE LEI:
Art. 1º. Fica instituída a Planta Genérica de Valores – PGV do Município de Iúna, constante no Anexo Único desta Lei complementar.
1º O valor venal dos imóveis situados no Município de Iúna será definido pelos algoritmos matemáticos, critérios, pesos e fórmulas detalhados na PGV constante no Anexo Único desta Lei complementar.
2º O Anexo Único contempla a PGV da Sede do Município. Os imóveis não contemplados no Anexo Único desta Lei complementar terão seus valores venais definidos pelos critérios, fórmulas, pesos e índices previstos na Lei nº 1.989, de 08 de dezembro de 2005 – Código Tributário Municipal.
3º Sempre que observada divergência entre o valor venal dado pelo § 1º e a realidade de mercado, o Órgão Tributário dará impulso a procedimento para sua atualização, observado o disposto no art. 54 da Lei nº 1.989, 2005 – Código Tributário Municipal.
Art. 2º. O art. 53 da Lei nº. 1.989, de 08 de dezembro de 2005, passa a ter seu caput com nova redação, passa a ter seu parágrafo único renumerado para § 1º e passa a vigorar acrescido de § 2º, nos seguintes termos:
“Art. 53. A base de cálculo do imposto é o valor venal do imóvel, que será determinado pela Planta Genérica de Valores – PGV em vigor no Município, conforme estabelecido em lei específica.
1º .......
2º Para os distritos, localidades e imóveis não contemplados pela PGV definida na forma do caput, os critérios para definição do valor venal do imóvel são os previstos neste Código, observado o disposto nos §§ 3º e 4º do art. 61.”
Art. 3º. O art. 61 da Lei nº. 1.989, de 08 de dezembro de 2005 passa a vigorar com a seguinte redação e acrescido dos parágrafos 1º, 2º, 3º e 4º:
“Art. 61. O valor do imposto será apurado mediante aplicação de alíquota sobre a base de cálculo, observados os seguintes índices:
I – para imóveis edificados, 0,1% (um décimo por cento) sobre o valor venal do imóvel;
II – para imóveis não edificados, 0,5% (cinco décimo por cento) sobre o valor venal do imóvel;
1º Fica concedido desconto sobre o valor do Imposto devido entre os exercícios de 2022 e 2029 nos seguintes percentuais:
I – no exercício de 2022, desconto de 50% (cinquenta por cento) do montante estipulado na forma do caput;
II – no exercício de 2023, desconto de 45% (quarenta e cinco por cento) do montante estipulado na forma do caput;
III – no exercício de 2024, desconto de 40% (quarenta por cento) do montante estipulado na forma do caput;
IV – no exercício de 2025, desconto de 30% (trinta por cento) do montante estipulado na forma do caput.
V – no exercício de 2026, desconto de 25% (vinte e cinco por cento) do montante estipulado na forma do caput.
VI – no exercício de 2027, desconto de 20% (vinte por cento) do montante estipulado na forma do caput.
VII – no exercício de 2028, desconto de 15% (quinze por cento) do montante estipulado na forma do caput.
VIII – no exercício de 2029, desconto de 10% (dez por cento) do montante estipulado na forma do caput.
2º A partir do exercício de 2030 o imposto será exigido em sua integralidade, na forma do caput.
3º Para os imóveis de que trata o § 2º do art. 53 deste Código, as alíquotas são de:
I – 0,5% (meio por cento) para imóveis edificados;
II – 2% (dois por cento) para imóveis não edificados.
4º O desconto conferido pelo § 1º não abrange os imóveis referidos no § 3º deste artigo.”
Art. 4º. O art. 83 da Lei nº 1.989, de 08 de dezembro de 2005, passa a vigorar com nova redação para a alínea c do inciso I e o § 1º, ambos do caput, e acrescido do parágrafo 5º, com a seguinte redação:
“Art. 83. .....
I - .....
c) alíquota de 5% (cinco por cento) para os itens 15 e 26 da lista de serviços.
1º As empresas prestadoras de serviços instaladas no Parque Industrial do Município terão alíquota de ISS de 2% (dois por cento) pelo período de 5 (cinco) anos, contados a partir da inscrição municipal, enquadrando-se, em seguida, no caput do art. 83 desta Lei.
....
5º A base de cálculo do ISS sobre serviços notarias e registrais (itens 21 e 21.01) é o valor dos emolumentos. O valor do imposto, que não compõe o valor do serviço, será destacado na respectiva nota pelo titular do cartório, que tem o dever de arrecadá-lo e repassá-lo ao Município até o dia 15 de cada mês.”
Art. 5º. A Lei n.º 1.989/2005, de 08 de dezembro de 2005, passa a vigorar acrescido do Art. 89-A, com a seguinte redação:
“Art. 89-A. Os registradores de imóveis fornecerão, mensalmente, até o último dia útil do mês subsequente à prática dos atos, informações sobre os registros referentes à transferência de propriedade de imóveis urbanos e de qualquer operação que seja fato gerador de tributo municipal, por meio de listagem, guias ou fotocópias de matrícula, em suporte físico ou eletrônico, conforme definido pela autoridade tributária competente.”
Art. 6º. Esta Lei Complementar entra em vigor na data de sua publicação.
Art. 7º Ficam revogada as disposições em contrário.
Gabinete do Prefeito Municipal de Iúna, Estado do Espírito Santo, aos vinte e dois dias do mês de dezembro do ano de dois mil e vinte e um (28/12/2021).
ROMÁRIO BATISTA VIEIRA
Prefeito Municipal de Iúna
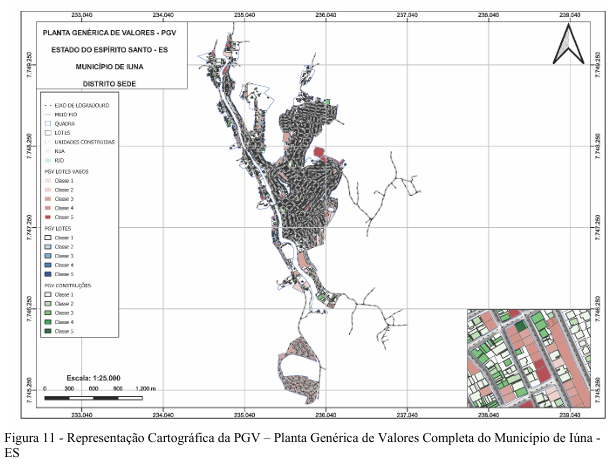
ANEXO ÚNICO
PLANTA GENÉRICA DE VALORES - PGV
MUNICÍPIO DE IÚNA - ES - SEDE
PGV EQUITATIVA – PLANTA GENÉRICA DE VALORES COM PRINCÍPIOS DE EQUIDADE IMOBILIÁRIA PARA O MUNICÍPIO DE IÚNA - ES
Pâmela Gurtel Tofoli – pamela.tofoli@ufv.br
Ataíde Luis de Oliveira – ataide.eng@gmail.com
Gérson Rodrigues dos Santos – gerson.santos@ufv.br
Jandresson Dias Pires – jandresson.pires@ufv.br
Ligia da Silva Barbosa – ligia.barbosa@ufv.br
Adriana M. Rocha Trancoso – adriana.trancoso@ufv.br
Lidiane Maria Ferraz Rosa – lidiane.rosa@ufv.br
Bruno dos Santos Ottoni – bruno.ottoni@ufv.br
RESUMO
Esse trabalho visa expor o método utilizado para atualização da Planta Genérica de Valores - PGV de um município de pequeno porte, com pouca infraestrutura para utilização de métodos estatísticos padronizados, estudados e aplicados em grandes municípios considerados referências destes que tem sido, na era moderna, a solução mais eficiência de equidade na arrecadação de tributos municipais, mais especificamente o Imposto Predial Urbano (IPTU). Muitos municípios do Estado do Espírito Santo tiveram seu crescimento econômico baseado no crescimento da produção cafeeira. Sua economia e o processo e aumento das produções nas fazendas e o desenvolvimento econômico de regiões vizinhas, criaram condições para a abertura de novas estradas, tornando-se intensa a relação comercial entre elas. Estes fatos atraíram transações imobiliárias que não seguem uma lógica, mas sim acompanham o crescimento da procura, alta especulação e praticamente nenhuma fonte de informação com critérios de mercado. Consequentemente, apesar dos cadastros imobiliários estarem em funcionamento, as informações dele e de mercado estão muitas vezes desatualizados e/ou com informações insuficientes para a formulação de qualquer modelo estatístico que garanta a confiabilidade da determinação dos valores. Foi então que o município de Iúna estabeleceu uma CTC - Cooperação Técnico-Científica com o Grupo de Pesquisa GeoTec/CNPq – Geociências Aplicadas e Tecnologias do IPPDS – Instituto de Políticas Públicas e Desenvolvimento Sustentável da UFV – Universidade Federal de Viçosa visando a realização do CTM – Cadastro Territorial Multifinalitário nos moldes da Portaria 511 de 2009, Lei 13.465 de 2017 e Decreto 9.310 de 2018 objetivando a atualização cadastral imobiliária da área urbana do município e produção da PGV com princípios científicos de equidade imobiliária. Para tanto, a NBR 14.653 de 2019 foi adotada, além da Geoestatística, Aprendizagem de Máquina e Geoprocessamento.
Palavras-chave: Planta de valores, IPTU, Cadastro imobiliário, Avaliação em Massa.
1. INTRODUÇÃO
O Imposto Predial e Territorial Urbano (IPTU) é um dos principais impostos municipais no Brasil e tem como fato gerador a propriedade urbana, sendo um mecanismo expressivo de arrecadação quando possui como base um Cadastro Imobiliário atualizado e confiável. Porém, nos pequenos e médios municípios, as dificuldades de administração tributária, bem como a vulnerabilidade política e pública dos critérios adotados, justificam o baixo desempenho de seu IPTU (GIFFONI e VILLELA, 1987, pg. 21). Na visão de Giffoni e Villela (1987, pg. 05), o baixo desempenho do IPTU também se deve a carência de recursos técnicos e humanos, dificuldade de atualizações cadastrais, somada ainda ao baixo valor venal apurado dos imóveis e períodos de inflação acentuada.
Para Möller (1995), citado por Moura e Carneiro (2002), a importância da manutenção e atualização dos cadastros imobiliários passaram a receber maior atenção dos municípios pequenos a partir da Lei de Responsabilidade Fiscal, uma vez que ela condicionou o recebimento pelos municípios de transferências voluntárias (oriundas dos governos estaduais e federais) ao zelo pela receita própria.
Os cadastros imobiliários são a base para apuração do valor venal de um imóvel, ao qual aplicada uma alíquota chega-se ao valor final do Imposto Predial e Territorial Urbano (IPTU), porém segundo Loch (2007) faltam leis cadastrais que direcionem e imponham ações mínimas para a implantação e atualização de projetos cadastrais, falta pessoal, equipes de geoprocessamento e software para a gestão da informação.
Segundo Vieira et.al (2002), as Plantas Genéricas de Valores - PGV surgem de uma composição de tabelas, listas, fatores corretivos e índices que, combinados, determinam os valores médios unitários (R$/m²) genéricos para a apuração do valor venal dos imóveis na face das quadras para fim de tributação. A finalidade principal de uma planta genérica de valores é fornecer os valores de mercado atualizados dos terrenos, quadra por quadra, ao longo dos logradouros de um determinado município (apud MOURA e CARNEIRO, 2002).
Alguns municípios, em especial, têm ainda mais dificuldade com atualização de suas plantas de valores, devido à alta especulação imobiliária, produto de inúmeras variáveis, escassas fontes de informação das transações imobiliárias por motivo de ausência de critérios justificáveis, ou seja, não existe uma lógica e sim o fluxo do aumento da procura e redução da oferta. Os municípios com grande progresso no potencial econômico e turístico possuem atrativos que chamaram a atenção do mercado imobiliário e o “boom” da valorização dos imóveis. Além disso, destaca-se a inflação acelerada que também tornou a PGV um instrumento pouco fiel à realidade, tornando necessárias atualizações periódicas e a criação de métodos condizentes.
Na região da rota turística imperial do estado do Espírito Santo, composta pelos municípios de Cariacica, Castelo, Conceição do Castelo, Domingos Martins, Iúna, Ibatiba, Ibitirama, Irupi, Muniz Freire, Viana, Santa Leopoldina, Santa Maria de Jetibá, Venda Nova do Imigrante e Vitória, os atrativos ambientais, boa qualidade de vida e clima, têm atraído pessoas de todas as regiões do estado, do Brasil e até de outros países para morarem ou investirem. Assim, o mercado imobiliário tem estado sempre aquecido, elevando os preços praticados sem uma escala lógica e sempre crescente.
Especificamente, o município de Iúna, está localizado a 184,7 quilômetros da capital Vitória, a uma altitude de 649 metros (IBGE, 2010). Em pesquisa realizada pelo Programa das Nações Unidas para o Desenvolvimento, divulgada no Atlas de Desenvolvimento Humano do Brasil (2000), Iúna possui 0,666 de IDH-M - Índice de Desenvolvimento Humano Municipal. Os índices avaliados foram: longevidade, mortalidade, educação, renda e sua distribuição.
Iúna contava com um sistema cadastral territorial, embora deficitário e no modelo tradicional do Boletim de Cadastro Imobiliário – BCI aos moldes antigos e manuais de desenho, com recursos humanos e computacionais. Seu Imposto Predial e Territorial Urbano (IPTU) era calculado a partir de mecanismos que não realçavam princípios de equidade imobiliária, padrão construtivo e infraestrutura oferecida, gerando assim muitas discrepâncias no processo de tributação imobiliária.
Através de uma CTC – Cooperação Técnico-Científica com o Grupo de Pesquisa GeoTec/CNPq – Geociências Aplicadas e Tecnologias do IPPDS – Instituto de Políticas Públicas e Desenvolvimento Sustentável da UFV – Universidade Federal de Viçosa o município realizou o CTM – Cadastro Territorial Multifinalitário nos moldes da Portaria 511 de 2009, Lei 13.465 de 2017 e Decreto 9.310 de 2018. Ademais, produziu-se uma PGV com princípios científicos de equidade imobiliária à luz da legislação vigente no país, NBR 14.653 de 2019, e um pacote metodológico que engloba Geoprocessamento, Sensoriamento Remoto, Aerofotogrametria, Geoestatística, Inteligência Geográfica e Inteligência Artificial – Aprendizagem de Máquina. Uma proposta de um modelo de atualização da PGV Equitativa foi desenvolvida para o município, observadas as peculiaridades do mesmo com o principal objetivo de corrigir a baixa avaliação imobiliária e atender o plano de ação do TCE-ES – Tribunal de Contas do Estado do Espírito Santo.
Este artigo apresenta a metodologia utilizada para a atualização da PGV do município, utilizando metodologias científicos que produzam a equidade imobiliária. Através de metodologias robustas presentes em Inteligência Artificial, Aprendizagem de Máquina, Geoestatística e Geoprocessamento, as especificidades do padrão construtivo, infraestrutura oferecida pelo município e demais caracterizações relevantes, construíram a Classificação Imobiliária da PGV Equitativa. Este pacote metodológico figura-se como a mais moderna modelagem científica, também chamada de Modelagem Híbrida. Em outras palavras, a modelagem híbrida é dada pela junção do que há de ótimo na modelagem tradicional (Estatística ou Matemática) e a robustez da Inteligência Artificial.
2. REFERENCIAL TEÓRICO
2.1.PLANTA GENÉRICA DE VALORES
Möller (1995) define Planta Genérica de Valores de terrenos como a planta do perímetro urbano onde são definidos os valores unitários do metro quadrado dos terrenos, para cada face de quadra, devidamente homogeneizados. Este autor define também Planta Genérica de Valores de edificações como um conjunto de valores unitários do metro quadrado para cada tipologia construtiva existente no perímetro urbano, passível de homogeneização, com relação aos seus diversos atributos, tais como localização, idade e estado de conservação, estes apurados em uma mesma data.
Uma das maiores dificuldades para atualizar a Planta Genérica de Valores, não é de caráter técnico, burocrático ou financeiro, mas sim político, em decorrência da dificuldade de negociação das prefeituras com as Câmaras Municipais para aprovação da referida Planta de Valores na forma da Lei (NADOLNY, 2016).
A NBR 14653-2 define planta de valores como a representação gráfica ou listagem dos valores genéricos de metro quadrado de terreno ou do imóvel numa mesma data, além de recomendar que a partir dos dados cadastrais, sejam realizadas vistorias por amostragem, com o objetivo de aferir os critérios e percepções considerados no cadastro. (ABNT, 2011).
Desta forma, para obter dados que reflitam a realidade, há a necessidade da aplicação de metodologias científicas, como a aplicação de procedimentos estatísticos, que proporcionem maior objetividade. No Brasil, a Associação Brasileira de Normas Técnicas (ABNT, 2011) estabeleceu regras específicas para a avaliação de imóveis urbanos, que é uma das etapas da geração da Planta Genérica de Valores. O método indicado para a elaboração de uma PGV é o método comparativo de dados de mercado (DALAQUA et al., 2010).
De acordo com Dalaqua et al. (2010), para o sucesso da aplicação deste método é necessário seguir alguns requisitos, que são: a existência de transações de imóveis que representem toda a variabilidade de valores da região a se gerar uma planta; dados referenciados à mesma época; e que sejam bem distribuídos espacialmente sobre a área de trabalho e em quantidade suficiente para possibilitar a análise dos valores.
É na planta genérica de valores que está definida a valoração dos imóveis de cada logradouro do município. Um problema recorrente na grande parte das cidades brasileiras é que os valores das plantas estão abaixo do valor de mercado, influenciando diretamente nas receitas municipais, especialmente o Imposto sobre Propriedade Predial e Territorial Urbana – IPTU. (SANTOS e NASCIMENTO, 2014).
Segundo Dalaqua et al. (2010), uma planta de valores bem elaborada consegue dar suporte ao órgão municipal em diversas atividades, especialmente a arrecadação via tributos imobiliários que engloba os impostos relacionados à transmissão de bens imóveis - ITBI e o imposto predial e territorial urbano – IPTU.
Sabe-se, portanto, que muitas cidades brasileiras mantêm um cadastro imobiliário técnico apenas para fins tributários e, na maioria das cidades de pequeno e médio porte, ainda subsiste o cadastro técnico analógico, expresso através de antigas tabelas e plantas manuais, onde são marcadas, de forma imprecisa e aleatória, as informações das alterações ocorridas ao longo do tempo sobre os imóveis. Não existe por parte da municipalidade a cultura de sistematização da informação com vistas à gestão territorial (OSÓRIO et al., 2012).
2.2. APRENDIZADO DE MÁQUINAS
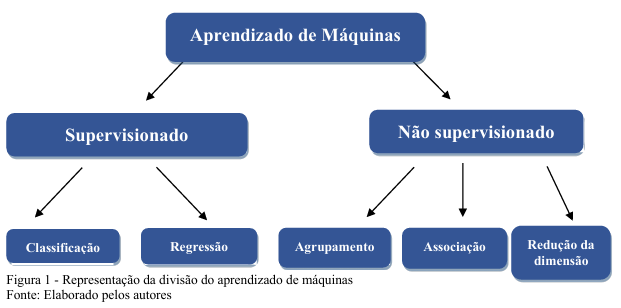
O aprendizado de máquinas (AM) é uma área da inteligiência artificial (IA) que tem por objetivo desenvolver técnicas computacionais capazes de resolver problemas automaticamente a partir de dados (BRINK e RICHARDS, 2013). Segundo Lorena e Carvalho (2007) AM é um conjunto de técnicas baseadas no princípio da indução e pode ser dividido em supervisionado ou não-supervisionado.
Segundo Brink e Richards (2013) “os algoritmos do aprendizado supervisionado são os mais comuns na área de Aprendizado de Máquinas”. De acordo com Monard e Baranauskas (2003a) o aprendizado supervisionado é aquele que apresenta ao algoritmo um conjunto de exemplos, em que é associado um rótulo a cada exemplo, ou seja, é apresentado ao conjunto de dados a resposta correta. O objetivo é partir de um conjunto de variáveis independentes para prever uma variável dependente, isto é, o conjunto de dados utilizados para o treinamento contém a variável resposta esperada.
Segundo Mitchell (1997) os exemplos podem apresentar uma ou mais características, e estas podem ser qualitativas ou quantitativas. Em relação aos rótulos, estes podem assumir valores contínuos ou discretos. Ao assumir valores contínuos o problema é resolvido com uma regressão, caso contrário, o problema é resolvido com uma classificação. Já no aprendizado de máquinas não supervisionado não existem exemplos rotulados. O objetivo do algoritmo é aprender a identificar tendências ou padrões que auxiliem na compreensão dos dados fornecidos (LORENA e CARVALHO, 2007). Nesse caso, são formados agrupamentos/clusteres que serão analisados e assim determinado o que significa cada agrupamento (MONARD e BARANAUSKAS, 2003a).
Na Figura 1 temos um esquema do aprendizado de máquinas.
Os algoritmos mais comuns de aprendizado de máquina para predições, apresentados na literatura, são: Random Forest; Support Vector Machine e Extra-Tree (HASTIE; TIBSHIRANI; FRIEDMAN, 2009; JAMES et al., 2013; CARVALHO, 2014). Entre os algoritmos de aprendizagem supervisionada destaca-se o Random Forest.
2.2.1. RANDOM FOREST
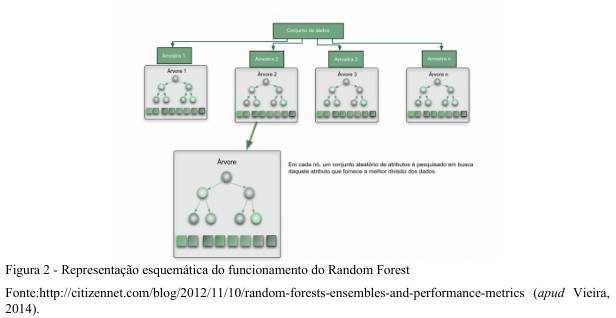
Random Forest (RF) é um algoritmo de aprendizado de máquina que foi desenvolvido por Breiman (2001). O destaque desse algoritmo está na utilização para predição de variáveis em diversos estudos, devido sua capacidade de seleção e classificação de preditores por importância (SUCHETANA, RAJAGOPALAN e SILVERSTEIN, 2017). Segundo Baker et al. (2014) o RF consiste em agrupar várias árvores de decisão obtidas a partir de um conjunto de dados de treinamento selecionados aleatoriamente utilizando a metodologia de divisão binária nas variáveis preditoras para classificar ou predizer valores de uma variável resposta (Figura 2).


2.2.2 SUPPORT VECTOR MACHINE (SVM)
Desenvolvida por Vapnik (1995), Support Vector Machine ou em português Máquina de Vetor Suporte, é uma técnica com base na Teoria de Aprendizado Estatístico que tem por objetivo resolver problemas de classificação de padrões e regressão (LORENA e CARVALHO, 2007). Essa técnica tem sido utilizada na categorização de textos (JOACHIMS, 2002) na análise de imagens (KIM et al. 2002), reconhecimento de objetos em 3 dimensões (Pontil e Verri, 1998), dentre outros.
Como exemplo de utilização da SVM podemos citar a diagnosticação de câncer de mama em um indivíduo. De forma bem sucinta, uma amostra celular de um paciente é classifícada ou como benigno ou como maligno (MENEZES, 2007).
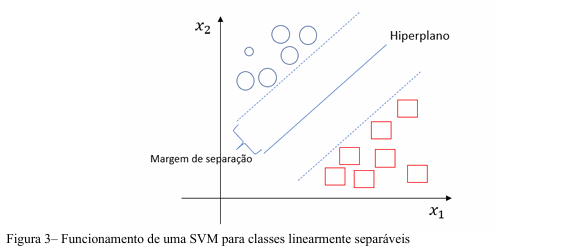
Algumas das características que tornam atrativa o uso da SVMs são boa capacidade de generalização e a robustez em grandes dimensões (SMOLA et al. 1999). Segundo Cosenza (2015) o procedimento para classificação baseia-se na separação ótima de um grupo de dados, independente de sua dimensão, com o objetivo de determinar um limite de decisão, conhecido como hiperplano, que separem os pontos de duas classes (LÁZARO, 2016). Esse hiperplano é orientado de forma que seja o mais próximo possível dos pontos na vizinhança de cada uma das classes. Esses pontos que tem a menor distância do hiperplano são denominados vetores de suporte LÁZARO).
De acordo com a Figura 3, temos a representação de duas classes linearmente separáveis e o hiperplano (linha) que as separa. A SVM determina o hiperplano que separa os pontos das duas classes de modo que o maior número de pontos da mesma fiquem do mesmo lado. O objetivo é que o hiperplano maximize a distância entre os pontos das classes. (Chaves, 2006).
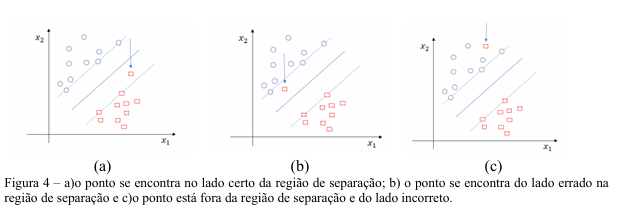
Porém, podem existir casos em que as classes não são linearmente separáveis. Sendo assim, o objetivo da SVM é descobrir um hiperplano que vá minimizar a probabilidade de erro de classificação junto com o conjunto de treinamento. Na Figura 4 tem-se três diferentes situações:
A finalidade da classificação é construir um modelo com capacidade de classificar novos objetos (com classe desconhecida) automaticamente de acordo com suas características, a partir de um banco de dados que contenha objetos com classe conhecida (préclassificados) (LÁZARO, 2016).
2.3. GEOESTATÍSTICA
O surgimento da Geoestatística dá-se no início na década de 1950, quando o engenheiro de minas sul-africano Daniel Krige, ao estudar o teor de ouro em jazidas, concluiu que as variâncias dos dados de concentração de ouro obtidas pela estatística clássica só faziam sentido se fosse considerada a distância entre os pontos amostrados (VIEIRA et al., 2000). A partir do trabalho de Krige, George Matheron, após apresentação de alguns trabalhos, formalizou, na década de 1960, a Teoria das Variáveis Regionalizadas (YAMAMOTO e LANDIM, 2013). Ele a definiu como sendo uma função espacial numérica, que varia de um local para outro, com continuidade aparente, cujos valores são relacionados com a posição espacial que ocupam e sua variação não pode ser representada por uma simples função matemática (MELLO et al., 2005).
A Geoestatística se diferencia da estatística clássica devido a existência de dependência espacial entre as amostras, ou seja, pela Teoria das Variáveis Regionalizadas há a pressuposição de que existe correlação entre os valores observados e a distância de onde os mesmos foram obtidos (MELLO et al., 2005). Esse conceito é utilizado na Geoestatística para predizer valores não amostrados. Para isso, duas ferramentas importantes são utilizadas: o semivariograma e a interpolação por krigagem (LANDIM, 1998).
O semivariograma é utilizado para estudar a similaridade entre amostras vizinhas, de forma que, observações mais próximas, são mais semelhantes entre si do que aquelas que estão separadas por distâncias maiores (SANTOS et al., 2011). De acordo com Vieira (2000), o estimador clássico do semivariograma é dado por:
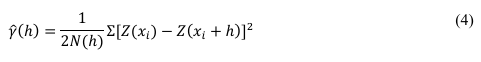
em que:
y(ℎ) é o valor estimado da semivariância para uma distância h;
z(xi) é o valor observado da variável no ponto (xi);
z(xi+ ℎ) é o valor observado no ponto (xi + ℎ);
ℎ é a distância entre os pares de casos amostrados;
N(ℎ) é o número de pares de pontos separados entre si por uma distância h.
O semivariograma é o gráfico que representa os valores das semivariâncias. Esta é uma função que só depende das distâncias entre os pontos amostrados e expressa a variabilidade espacial entre os mesmos (ISAAKS e SRIVASTAVA, 1989). Existem 3 (três) tipos de semivariogramas: o experimental, o verdadeiro e o teórico. Porém apenas o variograma experimental é conhecido na prática. Já o semivariograma teórico é uma referência para estimar o variograma verdadeiro. Na Figura 5 temos a representação dos três tipos de semivariograma (GUERRA, 1988).
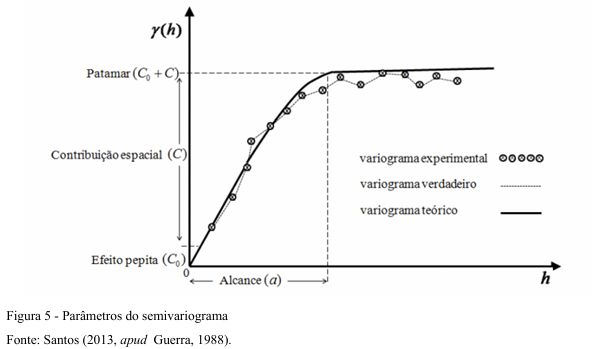
Conforme a Figura 5, com o ajuste do modelo teórico ao semivariograma experimental estima se alguns parâmetros, definidos por Isaaks e Srivastava (1989) por:


Diferentes modelos teóricos podem ser ajustados a um semivariograma experimental. Todavia, os modelos mais utilizados são: esférico, exponencial e gaussiano, apresentados nas equações (10), (11) e (12), respectivamente.
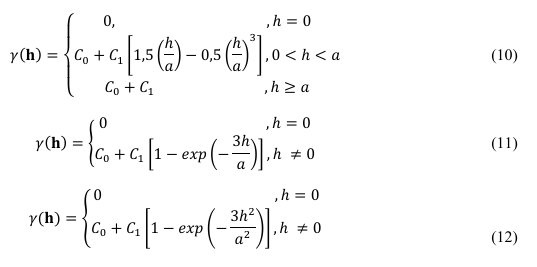
Como mencionado anteriormente, a interpolação na Geoestatística é feita por krigagem. Esse método permite predizer valores em pontos não amostrados por meio de pontos amostrados, levando em consideração a dependência espacial entre as amostras (ISAAKS e SRIVASTAVA, 1989). De acordo com Andriotti (2013) a krigagem considera: o número de amostras utilizadas, as posições destas na área a ser avaliada, as distâncias entre as amostras e a área a ser estimada e a continuidade espacial da variável em estudo. O estimador da krigagem é dado por,
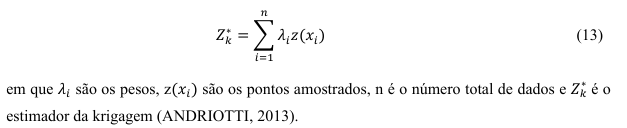
São encontrados diversos tipos de krigagens na literatura: krigagem simples, krigagem ordinária, krigagem universal, entre outras. Porém, segundo Santos et al. (2011) a krigagem simples é a mais precisa dentre os preditores lineares. Nesse trabalho será feita uma apresentação resumida sobre a Krigagem Simples e Ordinária. A Krigagem Simples (KS) é o método de estimação da Geoestatística em que se assume a função média do processo estocástico como conhecida (SANTOS et al., 2011) e o peso da média fornece um critério que permite testar a qualidade da krigagem (ANDRIOTTI, 2013). De acordo com Cressie (1993) este é o caso mais simples de previsão geoestatística que pode ser introduzido como preditor heterogeneamente linear (LIGAS e KULCZYCKI, 2010). Esse método de interpolação foi utilizado por Rosa (2017) para determinar o mapa de distribuição espacial da variável altimetria. Já a krigagem ordinária é o método que não é necessário que se conheça a média estacionária, sendo essa a mais utilizada devido essa característica (SANTOS et al., 2011). De acordo com Andriotti (2013), essa krigagem estima em qualquer lugar exceto nos pontos amostras em que são considerados os valores medidos.
3. CARACTERIZAÇÃO DA REGIÃO ESTUDADA
3.1.ROTA IMPERIAL
Nos últimos anos o turismo se destaca como um dos setores socioeconômicos mais significativos do mundo, incluindo as viagens de negócios, visita a amigos e familiares, viagens por motivações de estudos, religião, saúde, eventos esportivos, conferências e exposições, além das tradicionais viagens de férias e lazer.
O governo do Estado do Espírito Santo, de modo a permitir uma maior arrecadação financeira em regiões (“microrregiões”) fora da Grande Vitória, criou as “Rotas Turísticas” que abrangem diversos municípios de forma sistemática e otimizada (SETUR, 2019).
Atualmente, a Rota Imperial do estado do Espírito Santo é composta pelos municípios: Cariacica, Castelo, Conceição do Castelo, Domingos Martins, Iúna, Ibatiba, Ibitirama, Irupi, Muniz Freire, Viana, Santa Leopoldina, Santa Maria de Jetibá, Venda Nova do Imigrante e Vitória. Essa região teve um crescimento acelerado do potencial turístico através do resgate histórico e o reconhecimento de uma cultura peculiar trazida por imigrantes de distintos países, além dos atrativos ambientais e a comprovada boa qualidade de vida, fatos estes que culminaram no crescimento do mercado imobiliário tem se aproveitado disso.
São muitas as características semelhantes dos municípios da rota turística imperial do Espírito Santo. Para o estudo delas foi realizada uma seleção com base nas distâncias para os municípios vizinhos.
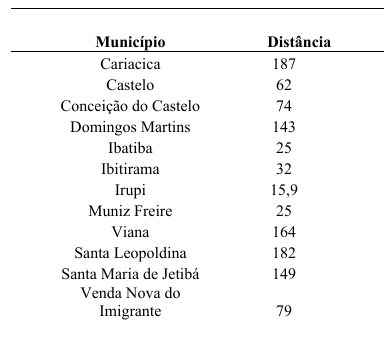

O município estudado possui atrativos que justificam o crescimento imobiliário que ocorreu nos últimos 10 anos, além disso, faz parte dos municípios de pequeno porte. Assim, seu mercado está mais baseado em métodos de mercado para avaliação de imóveis, gerando grandes dificuldades nas gestões de acompanharem estatisticamente, a atualização de suas PGVs.
3.2.O MUNICÍPIO DE IÚNA – ES
O município está localizado no sul do estado do Espírito Santo, integra a microrregião do Caparaó e está localizado à 184,7 km da capital do estado, Vitória. Possui uma área territorial de 460.365 km² e uma população estimada em 27.328 habitantes.
O IDH-M (Índice de Desenvolvimento Humano Municipal) possui um coeficiente de 0,666, sendo, portanto, inferior à média capixaba que é de 0,740 (PNUD, 2010).
O município está localizado em região de topografia acidentada, sendo atravessado pela serra do Caparaó, a oeste, junto à divisa com Minas Gerais; serra do Desengano, ao sul; serra do Valentim, a leste; e serra do Criciúma, ao norte (INCAPER, 2020). Possui um relevo que varia de fortemente ondulado a montanhoso. O município de Iúna possui as principais atividades econômicas divididas em: Agricultura, Agropecuária, Indústria e Serviços (Administração, Educação, Saúde Públicas e Seguridade Social)
O município, além de destacar-se pela produção cafeeira, pertence à Região do Caparaó, que cresce a cada dia para o turismo, mesmo que ainda discreto se comparado às demais rotas turísticas do estado do Espírito Santo. Possui nítida influência de países da Europa, conforme pode-se notar nos traços físicos de seu povo. Isso enriquece sua cultura e enobrece os capixabas e principalmente os visitantes que partilham desta vivência (GUIA TURÍSTICO E COMERCIAL ES, 2021).
A Rota do Caparaó é composta por onze municípios que oferecem diversas opções de turismo, como: aventura, ecoturismo, rural, religioso, cultural, gastronômico e de negócios e eventos. O turismo de negócios é o mais forte da região, devido às potencialidades econômicas concentradas nos mercados de mármore e granito, confecções e vestuário e produção rural diversificada. As belezas naturais e os atrativos, principalmente religiosos, se destacam na região (SETUR, 2021).
Todas as características do município apresentadas, associadas ao anseio moderno por sossego aqueceram o mercado imobiliário, as ofertas de emprego e oportunidade de negócios, atraindo trabalhadores e empresários e, por consequência, houve um crescimento acentuado e irregular das vendas de imóveis urbanos e rurais.
O valor real de mercado dos imóveis aumentou e, por consequência, se fez necessária a correção do valor venal através da PGV.
4. NOVA PLANTA GENÉRICA DE VALORES DO MUNICÍPIO DE IÚNA - ES E AVALIAÇÃO EM MASSA DE IMÓVEIS NOS TERMOS DA NBR 14653
Segundo Almeida (2006), a partir de 1999, iniciou-se um profundo trabalho de revisão das normas de avaliações brasileiras, dentre elas, a NBR 5676-Avaliação de imóveis urbanos, em vigência a partir de 1989, que sucedeu a NB-502 (1977), primeira norma a tratar de avaliações de imóveis urbanos, e, até então, principal referência para as avaliações imobiliárias.
Esta Planta Genérica de Valores aborda as etapas fundamentais da avaliação de um determinado imóvel urbano em um contexto geral do município, partindo dos dados de cadastro imobiliário, demonstrando a aplicação da Norma Brasileira para Avaliação de Bens, NBR 14653, em suas Partes 1 – Procedimentos Gerais e 2 – Imóveis Urbanos, que veio substituir as citadas NBR5676 de 1989.
A Portaria nº 511 de 2009 do Ministério das Cidades evidencia que a avaliação de imóveis é um processo técnico para fornecer o valor venal dos imóveis de um Município, servindo como base para o cálculo do Imposto Predial e Territorial Urbano – IPTU, além de outros tributos imobiliários.
A referida Portaria ainda recomenda em seu artigo 30, que o resultado do valor venal retrate o valor real do imóvel e seja revisado de quatro em quadro anos em municípios acima de 20.000 habitantes como Iúna, conforme dados do IBGE (2021) e de quatro em quatro em municípios, abaixo de 20.000 habitantes e que não evidenciam variação significativa nos valores dos imóveis, comprovada por meio de relatórios e pareceres técnicos, isto para promover o tratamento isonômico, justiça tributária, promoção da justiça fiscal e social e ainda ilustrar a dinâmica heterogênica do mercado imobiliário.
No que diz respeito ao intervalo de confiança e arbítrio, a NBR 5676, já cancelada e substituída, dispôs que “O valor final da avaliação, a ser indicado pelo engenheiro de avaliações em função do tratamento estatístico adotado, tem de estar contido em um intervalo de confiança fechado e máximo de 80%”, ou seja, facultava ao engenheiro avaliador essa margem de erro e confiança. Em outro ponto da Norma ainda trazia mais autonomia, admitindo que o próprio engenheiro definisse os limites dos intervalos de confiança inferidos de tratamento estatístico e indicasse a faixa de variação de preços do mercado que entendesse tolerável em relação ao valor final (GIANNAKOS e LEÃO, 1996).
A NBR vigente, nº 14.653-1, trata o intervalo de confiança e arbítrio como ‘campo de arbítrio’, isto em seu item 3.8, definindo-o como o intervalo de variação no entorno do estimador pontual adotado na avaliação, dentro do qual pode-se arbitrar o valor do bem, desde que justificado pela existência de características próprias não contempladas no modelo (ABNT, 2001).
A NBR vigente, nº 14.653-2 em seu item 8.2.1.5 estipula 15% de variação para mais ou para menos entorno da estimativa de tendência central utilizada na avaliação (ABNT, 2011).
A Portaria nº 511 de 2009 do Ministério das Cidades, por sua vez, estabelece de forma recomendatória o intervalo de confiança, que deverá ser de até 30% a menos e nunca mais do que o valor real de mercado, ressaltando ainda que uma dispersão superior a este intervalo incorre em falta de homogeneidade:
Art. 30. [...] § 4º O nível de avaliação é definido como a média dos quocientes dos valores avaliados, conforme constam no cadastro fiscal, em relação aos preços praticados no mercado para cada tipo de imóvel. A ocorrência de nível de avaliação para cada tipo de imóvel inferior a 70% (setenta por cento) ou acima de 100% (cem por cento) indica a necessidade de atualização dos valores.
§ 5º A uniformidade é definida pelo coeficiente de dispersão dos valores, que se traduz como o percentual médio das variações, em módulo, dos valores avaliados em relação aos preços praticados no mercado, para cada tipo de imóvel. A ocorrência de coeficiente de dispersão para cada tipo de imóvel superior a 30% (trinta por cento) indica falta de homogeneidade nos valores e a necessidade de atualização. (Portaria MCid nº 511 de 07/12/2009).
Em relação a identificação do valor de mercado do bem, a NBR 14653-1 traz em seu item 7.7.1 que deve ser feita de acordo com a aplicação da metodologia no tratamento dos dados de acordo com sua natureza, que por sua vez só pode ser conhecida a partir do diagnóstico de mercado de que trata o item 7.7.2 da Norma, este pode ser realizado de acordo com a estrutura de mercado encontrada (ABNT, 2001).
De acordo com a Portaria nº 511 de 2009 do Ministério das Cidades, o campo amostral e os valores de mercado do bem, para uma avaliação em massa do tipo PGV, será conhecido a partir de um cadastro multifinalitário fidedigno:
Art. 31. Recomenda-se que o Município forneça informações claras e precisas dos dados físicos e do valor do imóvel ao contribuinte, facilitando o atendimento a esclarecimentos e reclamações decorrentes do CTM e da avaliação dos imóveis.
A Norma estabelece as generalidades do bem avaliado como uma parte importante e anterior à escolha da metodologia aplicável, o item enfatiza que esta dependerá da natureza do bem avaliando, da finalidade da avaliação e da disponibilidade, qualidade e quantidade de informações colhidas no mercado, ainda que a escolha deverá ser justificada com o objetivo de retratar o comportamento do mercado por meio de modelos que suportem racionalmente o convencimento do valor (ABNT, 2001).
No caso de avaliações em massa, por se tratar de um campo amostral muito grande, usualmente a metodologia aplicável de acordo com as generalidades é o método comparativo direto de dados de mercado (item 8.2.1 NBR 14653-1), que identifica o valor de mercado do bem por meio de tratamento técnico dos atributos dos elementos comparáveis, constituintes da amostra, fica claro porém que o método por si só não seria suficiente, uma vez que seria humanamente impossível a avaliação de um montante tão robusto (DALAQUA et al., 2010).
A NBR 14653 em sua Parte 2: Avaliação de Imóveis Urbanos, traz as especificidades a serem utilizadas na avaliação em massa, planta de valores. Conforme o item 7.3.5.3, a vistoria ocorrerá por amostragem, para definição dos critérios do cadastro:
7.3.5.3. Planta de Valores: Nas avaliações em massa, a partir de dados cadastrais, recomenda-se vistoria por amostragem, com o objetivo de aferir os critérios e percepções consideradas no cadastro.
Ainda em relação ao método comparativo de dados de mercado, na estrutura da pesquisa serão levadas em consideração as variáveis relevantes na tendência de mercado, sendo que as variáveis independentes são os dados do cadastro e a dependente o preço de metro quadrado relativo a elas. Depois de realizado o levantamento das variáveis dependentes, no cadastramento imobiliário, estas são tratadas preliminarmente para definição da fórmula que resulta o valor venal/real (ABNT, 2011).
A utilização do Método Comparativo Direto de dados de Mercado consiste, portanto, no tratamento por fatores aplicável a uma amostra composta por dados de mercado, com características mais próximas possíveis ao imóvel avaliando, atendendo as exigências técnicas preconizadas pela NBR 14.653 – 2: Avaliação de Imóveis Urbanos.
A Planta Genérica de Valores do Município está inserida no Código Tributário Municipal, Lei nº 148, de 23 de dezembro de 1997, este define em seu artigo 121 a forma de atualização anual dos valores venais dos imóveis para fins de IPTU:
Art. 121. Caberá o órgão tributário elaborar propostas de atualização do valor venal dos imóveis para efeito de cálculos sobre o imposto sobre a Propriedade Predial e Territorial Urbana do exercício seguinte, com base nos estudos, pesquisas sistemáticas de mercado e análise respectivas, e encaminhá-la ao Gabinete do Prefeito, até o final de novembro de cada exercício civil (IÚNA, 1997).
São estabelecidos ainda critérios prévios para essa precificação anual:
§ 1º A proposta discriminará:
I – em relação aos terrenos;
a) o valor unitário, por metro quadrado ou por metro linear de testada, atribuído aos logradouros ou parte deles;
b)a indicação dos fatores corretivos de área, testada, forma geométrica, situação, nivelamento, topografia, pedologia e outros que venham ser utilizados, a serem aplicados na individualização dos valores venais dos terrenos.
II – em relação as edificações;
a)a relação dos diversos tipos de classificação das edificações, por uso, com indicações sintéticas das principais características físicas de cada tipo, registradas no Cadastro Imobiliário Tributário.
b) o valor unitário, por metro quadrado de construção, atribuído a cada um dos tipos de classificação das edificações;
c) a indicação dos fatores corretivos de posicionamento, idade de construção e outros que venham a ser utilizados, a serem aplicados na individualização dos valores venais das edificações.
§ 2º O encaminhamento da proposta será acompanhado de justificativas dos segmentos que conduziram à classificação das edificações, à indicação dos fatores corretivos e à fixação dos valores unitários.
§ 3º Na justificativa deverão ser demonstrados, entre outros:
I – a correlação significativa entre os valores fixados e as de mercado;
II – os níveis e as prováveis causas de variação, positiva ou negativa, dos valores fixados em comparação com os do período anterior;
III – as fontes de pesquisa do mercado imobiliário e publicações técnicas consulta e sua periodicidade (agentes financeiros de habitação, sindicatos de construção civil e outras entidades).
A avaliação em massa proposta neste trabalho foi fiel a NBR e aos critérios estabelecidos por esta Lei, sendo subdividida em sete etapas:
| 1ª Etapa | Validação do Método Comparativo de Dados de Mercado |
| 2ª Etapa | Definição das fórmulas de valor venal com variáveis relevantes do cadastro imobiliário atualizado |
| 3ª Etapa | Aplicação da fórmula em 50 amostras de lotes e construções |
| 4ª Etapa | Aplicação da fórmula para 1465 amostras de lotes |
| 5ª Etapa | Aplicação da fórmula para 5118 amostras de construções |
| 6ª Etapa | Treinamento da Inteligência Artificial para o processo de inferência |
| 7ª Etapa | Validação em campo das Plantas Genéricas de Valores |
4.1.PRIMEIRA ETAPA: VALIDAÇÃO DO MÉTODO COMPARATIVO DE DADOS DE MERCADO
Foram analisadas 16 (dezesseis) amostras de imóveis, entre edificados ou não, pertencentes ao bairro Nossa Senhora da Penha, coletadas da planta cadastral do município de Iúna – ES, com objetivo de comparação por homogeneização de fatores em relação ao imóvel avaliando, o Lote nº 91, com área de 163,57 m², topografia plana e localização A.
4.1.1. Descrição das Variáveis Dependentes e Independentes:
A partir da identificação da dinâmica de mercado através de seu diagnóstico nos termos do item 7.7.2 da NBR foram definidas as variáveis independentes relevantes na tendência de mercado:
4.1.1.1.Fator oferta ou transação (Foferta): Fator referente à condição do dado de mercado. Considerou-se na análise as amostras como fator oferta, tendo em vista que as mesmas foram coletadas da planta cadastral do município de Iúna – ES.
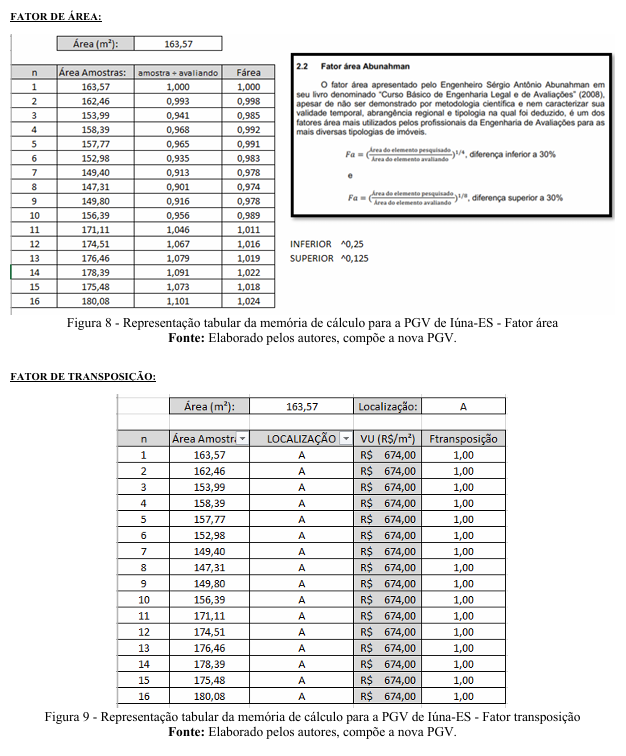
4.1.1.2.Fator área (Fárea): Fator referente à metragem da amostra (imóvel). Considerou-se na análise o fator área apresentado pelo Engenheiro Sérgio Antônio Abunahman em seu livro denominado “Curso Básico de Engenharia Legal e de Avaliações” (2008), apesar de não ser demonstrado por metodologia científica e nem caracterizar sua validade temporal, abrangência regional e tipologia na qual foi deduzido, é um dos fatores área mais utilizados pelos profissionais da Engenharia de Avaliações para as mais diversas tipologias de imóveis.

4.1.1.3. Fator Topografia (Ftopografia): Fator referente à topografia do imóvel sendo plano ou aclive/declive.
4.1.1.4. Fator transposição (Ftransposição): Fator referente à condição de explicar a localização dos imóveis. Considerou-se na análise as amostras como Fator transposição - localização A, tendo em vista se tratar de amostras coletas apenas num bairro específico do município.
Em seguida foi coletada a variável dependente para homogeinização:
4.1.1.5.VU (R$/m²): Valor unitário correspondente ao metro quadrado de área do imóvel (terreno). Considerou-se o valor unitário inicial a R$ 674,00 por metro quadrado. Valor arbitrado como parâmetro levando-se em consideração o valor praticado atualmente no município de Iúna- ES, em relação ao valor venal de imóvel.
A fórmula final representa a referida homogeinização por tratamento de fatores para obtenção do ‘Vu Homogeneizado’, também dado em R$/m²:
![]()
4.1.2. Critérios de Saneamento:
Após a homogeinização foram utilizados critérios estatísticos consagrados de eliminação de dados discrepantes, para o saneamento da amostra: critério de chauvenet, da média e do desvio padrão. Os dados discrepantes foram retirados um a um, do início pelo que esteja mais discrepante da média. Admite-se a reintrodução de dados anteriormente retirados no processo.
4.1.3. Memória de Cálculo:
Todos os cálculos foram realizados através de uma planilha, cuja memória pode ser conferida nas transcrições a seguir:
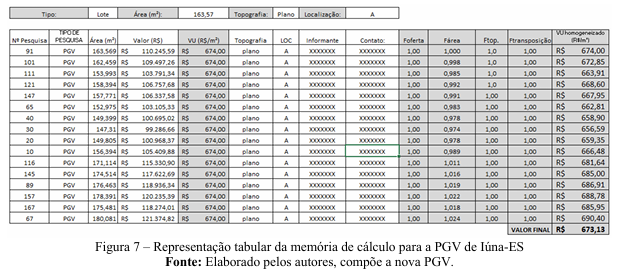
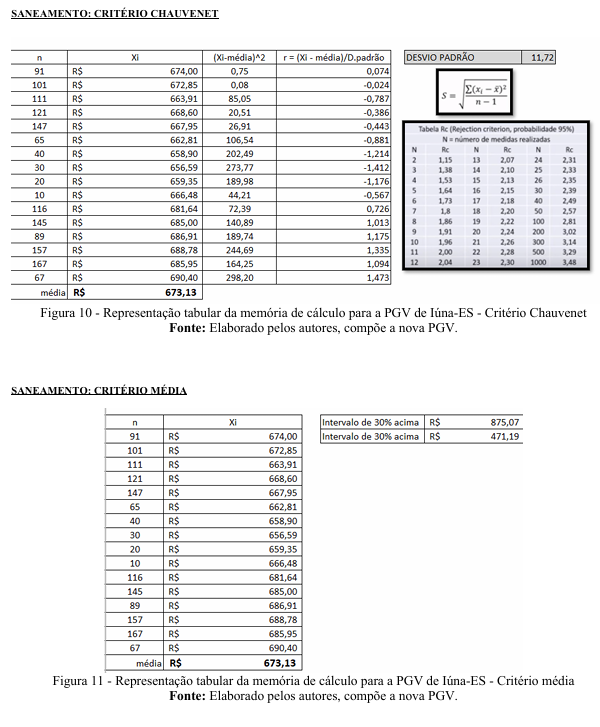
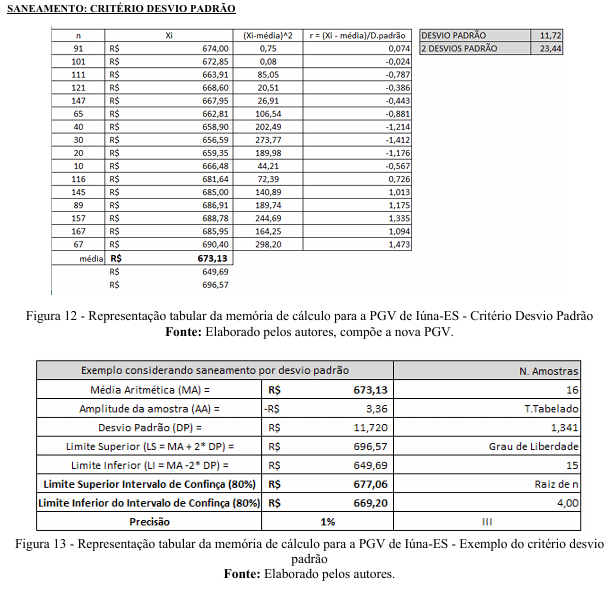
Por se tratar de situação hipotética a partir de análise de dados amostrais coletados da planta cadastral do município de Iúna – ES em consoante as exigências da NBR 14.653-2, concluímos que foi alcançado o Grau Precisão III e Grau de Fundamentação II.
4.2.SEGUNDA ETAPA: DEFINIÇÃO DAS FÓRMULAS DE VALOR VENAL COM VARIÁVEIS RELEVANTE DO CADASTRO IMOBILIÁRIO
Aplicaram-se as fórmulas padrões das avaliações em massa para melhor compreensão dos resultados obtidos no Método.
![]()
Sendo, o ‘Vb’ referente ao Valor Base e equiparado ao Valor unitário arbitrado no mercado imobiliário de R$ 638,40; o ‘Floc’ referente ao fator localização, que por se tratar do mesmo bairro foi arbitrado como 1,00; além dos fatores situação (S); pedologia (P) e topografia (T), de acordo com os dados do cadastro imobiliário e seguindo os seguintes fatores arbitrados:
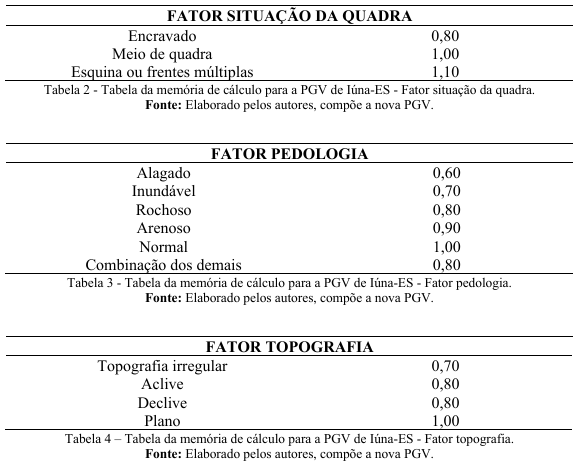
As tabelas acima compõem a PGV, sendo que o S – fator situação de quadra possui conceito de variação de 10% para mais ou 20% para menos do valor venal; o P – fator pedologia varia apenas a menor de no máximo 40%; e o T – fator topografia varia a menor de no máximo 30%.
Já a fómula de valor venal de edificação foi escrita para atender pressupostos teóricos dentro de um intervalo de confiança usual e ainda assim ser resumida em uma função dentro da generalidade que a NBR trás como metodologia aplicável da finalidade da avaliação e da disponibilidade, qualidade e quantidade de informações colhidas no mercado, uma vez estar convencionado nos projetos e Boletins de Cadastro Imobiliário, variáveis mais significativas e menos significativas, sendo as menos significativas trabalhadas na forma de média (Tr, Tp, Tc, Te, Is e Ie), ficanto a fórmula escrita da seguinte maneira:

Sendo, ‘Vm²e’ o valor do metro quadrado da edificação; ‘Ct’ o Coeficiente por tipo de edificação; ‘Tr’ o Tipo de revestimento externo; ‘Tp’ o Tipo de piso; ‘Tc’ o Tipo de cobertura; ‘Te’ o Tipo de estrutura; ‘Is’ o Tipo de instalação sanitária; ‘Ie’ o Tipo de instalação elétrica; ‘E’ o Estado de conservação; ‘St’ o Situação da edificação, e ‘Au’ a área da unidade.
No que tange o valor do metro quadrado da edificação, trata-se de valor de construção a ser corrigido pelo coeficiente por tipo de edificação (Ct). Contou com uma composição dos valores do CUB (Custo Unitário Básico) da publicação do SINDUSCON/ES (Sindicato da Construção Civil do Espírito Santo) e do Índice Nacional da Construção Civil (INCC), calculado pelo Instituto Brasileiro de Geografia e Estatística (IBGE), ambos para o mês de janeiro de 2021, corrigido a partir do arbitramento técnico do tipo de construção.
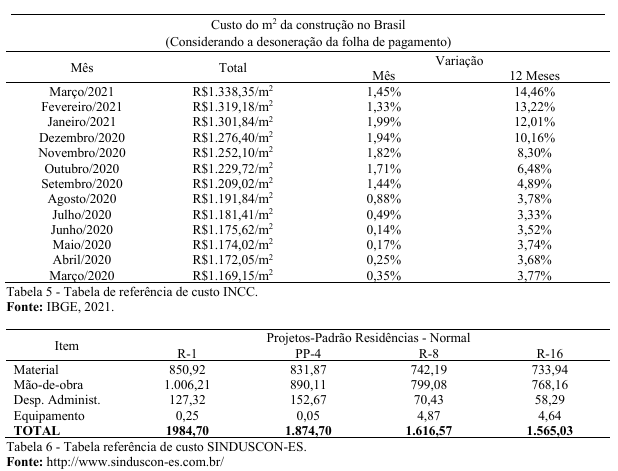
O valor médio do CUB utilizado foi a média aritmética dos Projetos Residenciais Padrões Normais referente ao mês de janeiro de 2021, R$ 1.760,25, uma vez que a diferenciação dos tipos das edificações será variada de acordo com a tabela de coeficiente por tipo de edificação (Ct). Vale ressaltar ainda que os valores de mercado usados foram os com a desoneração da folha de pagamento, por arbitramento e bem inferior a margem de 30%, de que trata a Portaria nº 511 MC e 15% que trata a NBR 14653-2. Foi então definido o Vm²e:
![]()
Para definir o coeficiente por tipo de edificação foi arbitrada variação percentual conforme a variação dos Projetos Padrões Normais apresentado nos CUBs de 29% das edificações residenciais e comerciais para galpoes e telheitos, 105% para edificações comercial e industrial e 118% das edificações residenciais e comerciais para edificações ditas especiais pelo BCI e com os valores médios padrão alto.
| TIPO DE EDIFICAÇÃO | ' CT ' |
| Residencial | 1,00 |
| Comercial / Industrial | 1,05 |
| Telheiro/ Galpão | 0,71 |
| Especial | 1,22 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
O coeficiente corretivo da categoria, usual em PGV foi substituído pela media aritmética das seis infraestruturas da edificação dada pela fórmula [(Tr+Tp+Tc+Te+Is+Ie)/6], por tratarem-se de variáveis menos expressivas, uma vez que a fórmula de gabaritos de pesos sobre 100, usual em Códigos Tributários, tem menor confiabilidade estatística, sendo que os pesos das variáveis são agora conhecidos a partir das seguintes tabelas:
| REVESTIMENTO EXTERNO ‘Tr’ |
| Especial | 1,10 |
| Sem revestimento | 0,70 |
| Emboço/reboco | 0,80 |
| Madeira | 0,90 |
| Pintura | 1,00 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
| TIPO DE PISO ‘Tp’ |
| Terra batida | 0,60 |
| Cimento | 0,70 |
| Tábuas/taco | 0,80 |
| Cerâmica | 1,00 |
| Especial | 1,10 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
| TIPO DE COBERTURA ‘Tc’ |
| Palha | 0,70 |
| Fibrocimento | 0,80 |
| Laje | 0,90 |
| Telha colonial | 1,00 |
| Especial | 1,10 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
| TIPO DE ESTRUTURA ‘Te’ |
| Madeira= 0,90 | 0,90 |
| Metálica= 0,90 | 0,90 |
| Alvenaria= 1,00 | 1,00 |
| Concreto= 1,10 | 1,10 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
| INSTALAÇÕES SANITÁRIAS ‘Is’ |
| Inexistente | 0,70 |
| Externa | 0,80 |
| Interna simples | 0,90 |
| Mais de uma interna | 1,00 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
| INSTALAÇÕES SANITÁRIAS ‘Ie’ |
| Inexistente | 0,80 |
| Aparente | 0,90 |
| Embutida | 1,00 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
A tabela de estado de conservação, dada por ‘E’, fica assim estabelecida:
| ESTADO DE CONSERVAÇÃO ‘E’ |
| Nova/ ótimo | 1,10 |
| Bom | 1,00 |
| Regular | 0,90 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
Por último, a variável situação da edificação (St) será definida através da tabela a seguir, não sendo diferenciada pelo tipo do imóvel, considerando que essa conversão já é realizada pela variável Ct (categoria da edificação):
| ESTADO DE CONSERVAÇÃO ‘E’ |
| Frente | 1,00 |
| Fundos | 0,90 |
Fonte: Elaborado pelos autores, compõe a nova PGV.
As tabelas apresentadas nesta sessão compõem a nova Planta Genérica de Valores do município de Iúna-ES, atualizada a partir de adaptações do Método Comparativo de Dados de Mercado, recomendado pela Norma Brasileira para Avaliação de Imóveis Urbanos e Portaria 511 de 2009 do Ministério das Cidades.
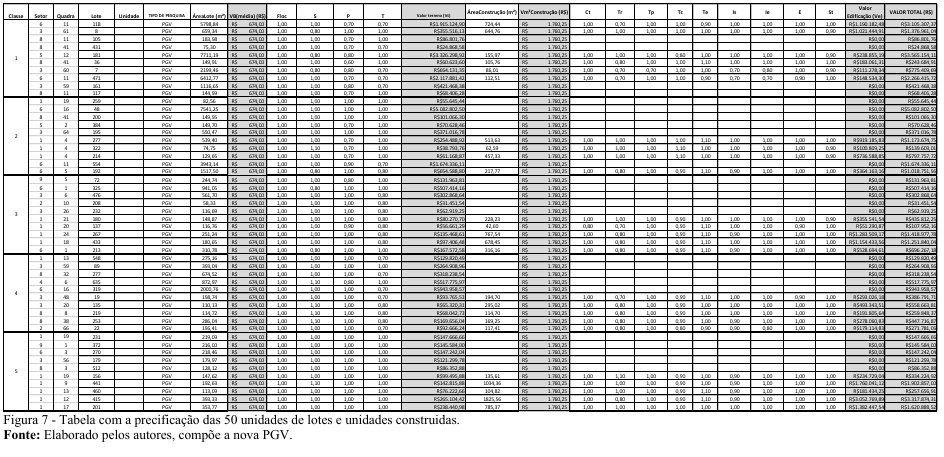
O resultado para as 50 amostras foi o seguinte:
4.3.TERCEIRA ETAPA: APLICAÇÃO DA FÓRMULA EM AMOSTRAS DE LOTES
Nesta etapa foi selecionada aleatoriamente uma amostra de 50 unidades de lotes e unidades construídas para estudo do valor venal.
5. METODOLOGIA DE GENERALIZAÇÃO DA NOVA PLANTA GENÉRICA DE VALORES DO MUNICÍPIO DE IÚNA - ES
De acordo com as prerrogativas e diante da generalidade prevista em Norma, o método comparativo de dados de mercado pode, na era moderna, se associar a ciência moderna da Geoestatística, responsável pela criação de zonas homogêneas e assumindo grupos setorizados. Para a comparação das avaliações de acordo com suas variáveis e, ainda, aplicação da Inteligência Artificial, via Aprendizagem de Máquina, responsável por classificar imóveis com muitas características, o objetivo maior é encontrar a equidade imobiliária, ou seja, encontrar seus pontos comuns da avaliação em massa.
Em relação a metodologia escolhida, a NBR 14653-1 abre em seu item 8.1.2 a possibilidade de o engenheiro de avaliações empregar outros procedimentos justificados, ou seja, muitas vezes complementar o método para as particularidades da avaliação (ABNT, 2001).
Para a atualização da Planta Genérica de Valores de Iúna-ES foram utilizados os princípios científicos de equidade imobiliária, aplicados conforme orientações da Portaria Federal nº 511 de 07 de dezembro de 2009, do Ministério das Cidades, através das metodologias da Geoestatística, principal ciência responsável pela criação de zonas homogêneas; Aprendizagem de Máquina, principal ciência responsável por classificar imóveis com muitas características a serem avaliadas e levadas em consideração; NBR 14.653 de 2011, procedimentos gerais de avaliação imobiliária em massa.
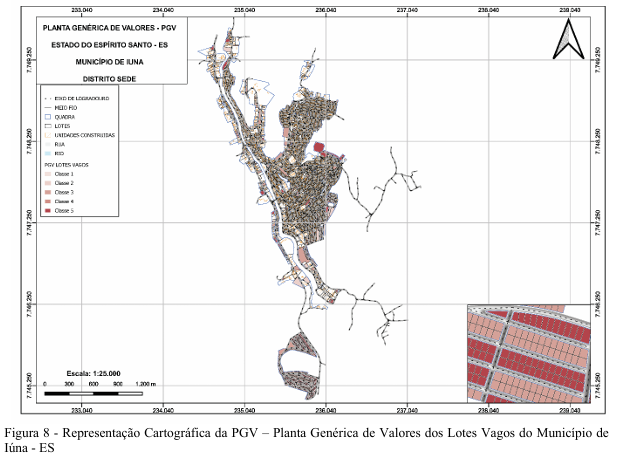
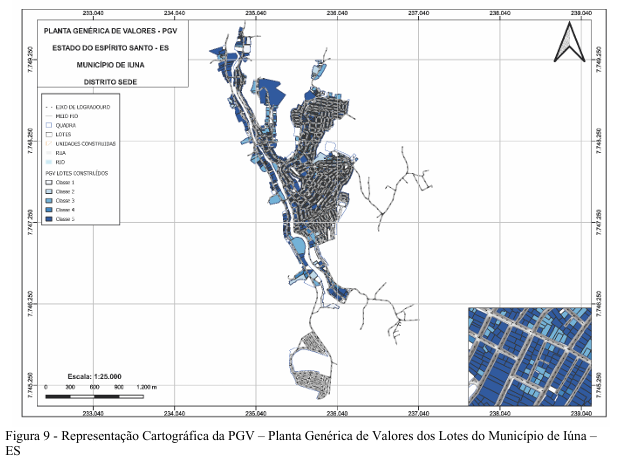
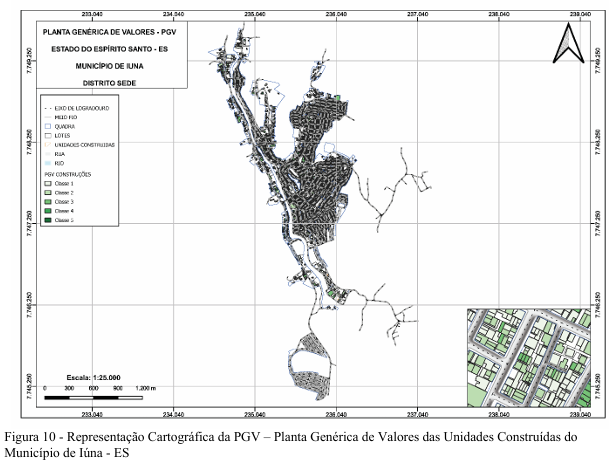
No que tange a Geoestatística e a Aprendizagem de Máquina, a classificação imobiliária contou com uma setorização de 1 a 4 e uma classificação de 1 a 5 para lotes, e com classificação de 1 a 5 para construções:
| 1. No centro Comercial: Ruas que compõem: Presidente Tancredo Neves, Galaor Rios. |
| LOTE: quando o lote possuir frentes múltiplas, topografia plano, possuir todos os equipamentos urbanos e não for alagável, ele é CLASSE 5; se o imóvel possuir apenas uma frente, for plano ou quase plano, possuir todos os equipamentos urbanos e não for alagável, será CLASSE 4; quando o imóvel possuir apenas uma frente, até 3 equipamentos urbanos, topografia aclive ou declive e não for alagável, será CLASSE 3; se o imóvel possuir apenas uma frente, topografia aclive ou declive, possuir menos de 3 equipamentos urbanos e for alagável, será CLASSE 2; se o imóvel for encravado, possuir até dois equipamentos urbanos. Topografia combinação e for alagável, será CLASSE 1. |
| 2. Bairros do entorno do Centro Comercial: (Bairros: Pito, Quilombo (parcial 50%). |
| LOTE: quando o lote possuir frentes múltiplas, topografia plano, possuir todos os equipamentos urbanos e não for alagável, ele é CLASSE 5; se o imóvel possuir apenas uma frente, topografia plano ou quase plano, possuir todos os equipamentos urbanos e não for alagável, será CLASSE 4; quando o imóvel possuir apenas uma frente, até 3 equipamentos urbanos, topografia aclive ou declive e não for alagável, será CLASSE 3; se o imóvel possuir apenas uma frente, topografia aclive ou declive, possuir menos de 3 equipamentos urbanos e for alagável, será CLASSE 2; se o imóvel for encravado, possuir até dois equipamentos urbanos, topografia combinação e for alagável, será CLASSE 1. |
| 3. Bairros periféricos e de apelo social: (Bairros: Quilombo (parcial 50%), Nossa Senhora da Penha, Guanabara (20%). |
| LOTE: quando o lote possuir frentes múltiplas, topografia plano, possuir todos os equipamentos urbanos e não for alagável, ele é CLASSE 5; se o imóvel possuir apenas uma frente, topografia plano ou quase plano, possuir todos os equipamentos urbanos e não for alagável, será CLASSE 4; quando o imóvel possuir apenas uma frente, até 3 equipamentos urbanos, topografia aclive ou declive e não for alagável, será CLASSE 3; se o imóvel possuir apenas uma frente, topografia aclive ou declive, possuir menos de 3 equipamentos urbanos e for alagável, será CLASSE 2; se o imóvel for encravado, possuir até dois equipamentos urbanos, topografia combinação e for alagável, será CLASSE 1. |
| 4. Bairros Especiais: (Bairros: Ferreira Vale, Vila Nova, Niterói, Guanabara (parcial 80%). |
| LOTE: quando o lote possuir frentes múltiplas, topografia plano, possuir todos os equipamentos urbanos e não for alagável, ele é CLASSE 5; se o imóvel possuir apenas uma frente, topografia plano ou quase plano, possuir todos os equipamentos urbanos e não for alagável, será CLASSE 4; quando o imóvel possuir apenas uma frente, até 3 equipamentos urbanos, topografia aclive ou declive e não for alagável, será CLASSE 3; se o imóvel possuir apenas uma frente, topografia aclive ou declive, possuir menos de 3 equipamentos urbanos e for alagável, será CLASSE 2; se o imóvel for encravado, possuir até dois equipamentos urbanos, topografia combinação e for alagável, será CLASSE 1. |
| CONSTRUÇÕES (não mudam por setor/bairro) |
| Classe 1 | • Casa/Especial/Prédio/Apartamento: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétricasem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular. • Telheiro: todos que não tenham instalações sanitárias e elétricas aparentes e de fundos. • Galpão/Indústria: todos que não tenham instalações sanitárias ou simples, elétricas aparentes, de alvenaria, sem revestimento, sem forro, situação fundos, posição alinhada e com estado de conservação mau ou regular. • Estacionamento/garagem: sem revestimento, com cobertura de palha. • Loja/Comércio/Escritório/Sala Comercial: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétrica sem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular, geminada ou conjugada. |
| Classe 2 | • Casa/Especial/Prédio/Apartamento: em sua maioria sendo de revestimento emboco/reboco, com piso de cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte, com instalação sanitária simples, instalação elétrica aparente, estrutura de alvenaria ou de madeira, situação frente, posição alinhada e com estado de conservação regular. • Telheiro: todos que tenham instalações sanitárias, elétricas aparentes e de frente. • Galpão/Indústria: todos que não tenham instalações sanitárias ou simples, elétricas aparentes, de alvenaria, sem revestimento ou com revestimento de madeira, sem forro, situação frente, posição alinhada e com estado de conservação regular.• Estacionamento/garagem: sem revestimento, cobertura de fibrocimento ou telha. • Loja/Comércio/Escritório/Sala Comercial: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétrica sem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular, geminada ou conjugada. |
| Classe 3 | Casa/Especial/Prédio/Apartamento: em sua maioria sendo de revestimento cerâmico, com forro de madeira ou PVC, com piso de cimento em sua maioria e alguns com cerâmica, cobertura de telha em grande parte, com instalação mais de uma interna, instalação elétrica embutida, estrutura de alvenaria ou concreto, situação frente, posição recuada e com estado de conservação bom. • Telheiro: todos que tenham instalações sanitárias, elétricas embutidas e de frente. • Galpão/Indústria: instalações sanitárias ou simples, elétricas embutidas, de alvenaria ou concreto, revestimento cerâmico, com forro, situação frente, posição recuada e com estado de conservação bom. • Estacionamento/garagem: com revestimento, cobertura de fibrocimento ou telha. • Loja/Comércio/Escritório/Sala Comercial: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétrica sem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular, superposta. |
| Classe 4 | Casa/Especial/Prédio/Apartamento: em sua maioria sendo de revestimento cerâmico, com piso de cimento em sua maioria e alguns com cerâmica, com forro de laje, cobertura de telha em grande parte e laje, com instalação mais de uma interna, instalação elétrica embutida, estrutura de concreto, situação frente, posição recuada e com estado de conservação ótimo. • Telheiro: nenhum. • Galpão/Indústria: instalações sanitárias ou simples, elétricas embutidas, de concreto, revestimento cerâmico, com forro, situação frente, posição recuada e com estado de conservação ótimo. • Estacionamento/garagem: nenhum. • Loja/Comércio/Escritório/Sala Comercial: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento em sua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétrica sem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular, isolada. |
| Classe 5 | Casa/Especial/Prédio/Apartamento: em sua maioria sendo de revestimento cerâmico, com piso de cimento em sua maioria e alguns com cerâmica, com forro de laje, cobertura de telha ou laje, com instalação mais de uma interna, instalação elétrica embutida, estrutura concreto, situação frente, posição recuada e com estado de conservação ótimo. • Telheiro: nenhum. • Galpão/Indústria: nenhum. • Estacionamento/garagem: nenhum. • Loja/Comércio/Escritório/Sala Comercial: em sua maioria sendo de revestimento sem ou emboco/reboco, com piso de terra batida ou cimento emsua maioria, sem forro, cobertura de fibrocimento em grande parte ou palha, sem instalação sanitária sem e alguns interna completa, instalação elétrica sem e alguns embutida e aparente, estrutura de alvenaria ou de madeira, situação fundos, posição alinhada e com estado de conservação mau ou regular, isolada. |
5.1.APRENDIZAGEM DE MÁQUINA PARA PRECIFICAÇÃO DOS IMÓVEIS
Após a avaliação e precificação de 50 imóveis para lotes e unidades construídas, conforme apresentado anteriormente, com o intuído de redução do erro amostral e aumento da acurácia da modelagem utilizou-se o software R versão 4.0.4 para replicar a precificação dos imóveis de acordo com as equações (15) e (16) para os cálculos dos valores venais de 1465 e 5118 amostras para lotes e unidades construídas, respectivamente. Em seguida, realizou o treinamento do algoritmo Random Forest (RF) de precificação em massa dos imóveis.
O modelo de florestas aleatórias foi estimado inicialmente sobre a base de dados para o aprendizado da máquina, citada anteriormente, cujo treinamento foi composto por 70% dos dados amostrais e o grupo de teste por 30% tanto nos lotes como nas unidades construídas. Foram utilizadas como preditoras as variáveis independentes: Classificação das Construções (Class_Const), Classificação dos Lotes (Class_Lote) e a área em m² das construções (ArConst) para precificar as unidades construídas; e as variáveis: Classificação dos Lotes (Class_Lote), Área total do terreno (ArTerreno) e Área total da construção (ArTotConst) para precificar os lotes. Por fim, após a validação dos dados gerou se a precificação em massa dos 4.884 Lotes e 17.058 unidades construídas contidas na base de dados.
6. RESULTADOS
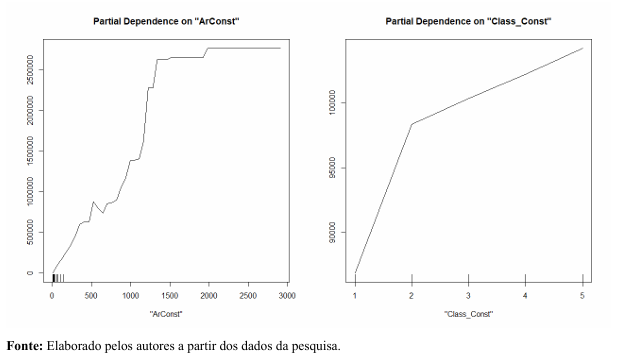
Os modelos em que envolvam árvores de decisão não permitem avaliar diretamente como cada preditor está associado com a variável resposta (Oliveira,2020), então com o gráfico de dependência parcial é possível avaliar esta associação visualmente. Esse gráfico mostra o efeito da marginal de um preditor no valor predito pelo modelo. A partir dele, é possível investigar qual a forma e o sentido da relação entre cada preditor e a variável resposta. Estes gráficos podem mostrar se essa relação é linear, monotônica ou mais complexa. (HASTIE; Tibshirani; Friedman, 2008, p. 369; Amorim, 2019, p.7 apud Oliveira, 2020). De acordo com o gráfico 01 vemos com destaque para o aumento do preço unitário à medida que se aumentam o tamanho da área das construções, apresentando alguns pontos de estabilidade, na qual destacamos, no valor após aproximadamentes 2000m², e as classes com um “acelerado” crecimento do valor quando se muda da classe 1 para a classe 2.
Gráfico 1 - Dependência parcial do preço unitário das construções com o modelo RF.
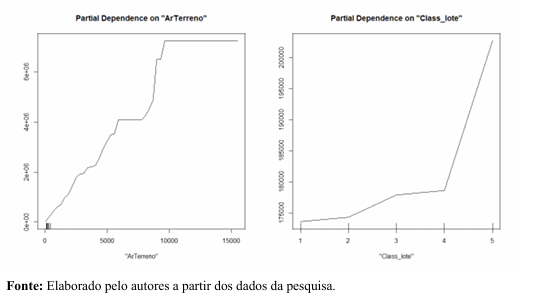
De acordo com o gráfico 2 nota-se o aumento do preço unitário do lote à medida que se aumentam o tamanho dos lotes, embora, há intervalos de valores constantes para o aumento da área do lote com destaque para áreas superiores a aproximadamente 10.000m². Quando se observa a dependência parcial das classes destaca-se o crescimento acelerado da classe 4 para a 5.
Gráfico 2 - Dependência parcial do preço unitário dos Lotes com o modelo RF.
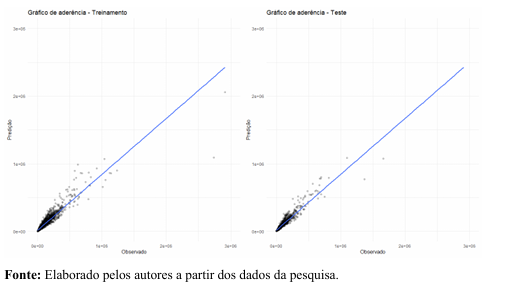
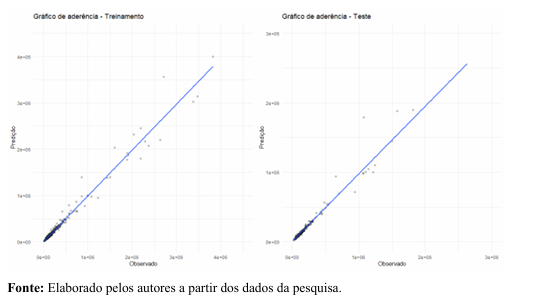
Através do Gráfico 3, à esquerda, também se observa a falta de ajuste em algumas construções com preços relativamente altos, entretanto, a aderência dos dados se mostra eficaz. O coeficiente de determinação (R²) para os dados out-of-bag foi de 0,877. Analogamente, no Gráfico 3, à direita, mostra a dispersão entre os valores observados e estimados sobre a base de teste. O coeficiente de determinação (R²) apresentado no modelo foi de 0,91.
Gráfico 3 - Dispersão do valor observado (R$) x valor predito (R$) do modelo RF sobre as amostras de treinamento e teste das unidades construídas.
Pelo Gráfico 4, à esquerada, nota-se a falta de ajuste em alguns lotes com preços relativamente altos ou baixos, no entanto, a aderência dos dados mostrou eficaz. O coeficiente de determinação (R²) para os dados out-of-bag foi de 0,945. Analogamente, no Gráfico 04, à direita, mostra a dispersão entre os valores observados e estimados sobre a base de teste. O coeficiente de determinação (R²) apresentado no modelo foi de 0,952.
Gráfico 4 - Dispersão do valor observado (R$) x valor predito (R$) do modelo RF sobre as amostras de treinamento e teste dos lotes.
Após o treinamento e validação dos modelos realizou-se a predição das 17058 unidades construídas e dos 4884 lotes no município de Iúna, cuja análise descritiva é apresentada nas tabelas apresentadas em seguida.
| Classe | N | Percentual | Média(R$) | CV | Mediana(R$) | Mínimo(R$) | Máximo(R$) |
| 1 | 11389 | 66,77% | 78.066,32 | 1,34 | 45.040,03 | 1.817.00 | 3.232.636,15 |
| 2 | 2050 | 12,02% | 127.761,72 | 1,42 | 85.219,89 | 3.377,94 | 4.991.887,90 |
| 3 | 3242 | 19,01% | 124.465,67 | 1,80 | 93.199,80 | 1.859,40 | 7.680.596,40 |
| 4 | 306 | 1,79% | 117.419,47 | 1,11 | 74.940,64 | 4.610,15 | 937.003,08 |
| 5 | 71 | 0,42% | 157.661,15 | 1,36 | 59.246,83 | 8.126,70 | 1.190.722,75 |
| Total | 17058 | 100% | 93.894,41 | 1,57 | 58.705,10 | 1.817.00 | 7.680.596,40 |
Fonte: Elaborado pelos autores a partir dos dados da pesquisa.
| Classe | N | Percentual | Média(R$) | CV | Mediana(R$) | Mínimo(R$) | Máximo(R$) |
| 1 | 19 | 0,4% | 1.050.819,52 | 1.49 | 352.123,07 | 31.240,27 | 4.468.343,48 |
| 2 | 184 | 3,77% | 377.762,90 | 2,55 | 104.512,36 | 10.986,50 | 7.228.696,95 |
| 3 | 986 | 20,19% | 232.307,43 | 3,51 | 96.989,25 | 4.140,44 | 17.034.683,25 |
| 4 | 220 | 4,50% | 172.228,46 | 2,22 | 68.332,55 | 5.180,95 | 3.917.195,07 |
| 5 | 3475 | 71,15% | 212.336,51 | 3,28 | 105.173,79 | 4.049,71 | 29.159.353,08 |
| Total | 4884 | 100% | 223.988,10 | 3,26 | 102.579,16 | 4.049,71 | 29.159.353,08 |
Fonte: Elaborado pelos autores a partir dos dados da pesquisa.

Para se testar se existe realmente diferenças estatísticas entre o observado e o predito, aplicou se o teste de postos sinalizados de Mann-Whitney-Wilcoxon que tem como hipótese nula (teste bilateral) a igualdade de medianas, e hipótese alternativa, a diferença delas. Este teste foi escolhido, dado a não normalidade observada na distribuição dos resíduos, segundo o teste de Anderson-Darling. Em todos os testes, realizados dois a dois, entre os conjuntos de treino, teste e todo o banco de dados não encontrou evidências para rejeitar a hipótese nula de que as medianas dos dados são iguais com significância de 5%. De certa forma, isso nos leva a concluir que não existem diferenças significativas entre as medianas dos valores preditos para os valores reais, ou seja, não há diferenças estatisticamente significantes em tais medidas, concluindo assim que os grupos são da mesma população.
7. CONCLUSÃO
A PGV - Planta Genérica de Valores de Iúna-ES adotou todas as etapas fundamentais da avaliação em massa de imóveis urbanos para a sede do município, conforme a NBR 14.653 de 2019, partindo da atualização cadastral imobiliária através de uma CTC - Cooperação Técnico Científica com o Grupo de Pesquisa GeoTec/CNPq – Geociências Aplicadas e Tecnologias do IPPDS – Instituto de Políticas Públicas e Desenvolvimento Sustentável da UFV – Universidade Federal de Viçosa visando a realização do CTM – Cadastro Territorial Multifinalitário nos moldes da Portaria 511 de 2009, Lei 13.465 de 2017 e Decreto 9.310 de 2018.
A PGV de Iúna-ES foi construída pautada no uso de princípios científicos de equidade imobiliária através de Aerofotogrametria, Geoprocessamento, Topografia, Geoestatística, Inteligência Artificial via Aprendizagem de Máquina e Avaliação em Massa de Imóveis. Após a atualização cadastral dos imóveis urbanos da sede do município, adotou-se 7 (sete) etapas, partindo da construção de fórmulas para o método comparativo, preconizado pela NBR, passando pelas etapas amostrais e de generalização populacional, até a validação em campo da classificação e precificação imobiliária.
O processo amostral passou por duas fases distintas, iniciando com um erro amostral controlado de 10% e concluindo com um erro amostral controlado de 2%. Já o processo de Inferência Estatística foi realizado por Inteligência Artificial via Aprendizagem de Máquina, treinamento este realizado pelos avaliadores em massa do projeto, e tendo como 95% e 92% de variação explicada para os lotes e construções, respectivamente.
Vários resultados foram gerados a partir deste projeto, a saber: banco de dados georreferenciados com características multiusuário, multicamada e multifinalitário; sistema de informação geográfica opensource; sistema de informação geográfica web; PGV para lotes vagos, PGV para lotes construídos e PGV para construções; plantas e memoriais para fins de Regularização Fundiária; e uma base sólida para o uso de inteligência geográfica em prol de uma cidade inteligente.
Finalmente, conforme recomenda a Portaria 511 de 2009, essa PGV deverá ser revisada de oito em oito anos em municípios abaixo de 20.000 habitantes e de quatro em quatro em municípios como Iúna, acima de 20.000 habitantes, conforme dados do IBGE, 2021. Contudo, evidenciando uma variação significativa nos valores dos imóveis, comprovada por meio de relatórios e pareceres técnicos, esta PGV poderá ser revista numa periodicidade menor, visando promover o tratamento isonômico de justiça tributária, da justiça fiscal e social e ainda ilustrar a dinâmica heterogênica do mercado imobiliário.
AGRADECIMENTOS:
Em primeiro lugar, agradecemos a Deus pelo dom da vida e oportunidade de produzir ciência de qualidade e aplicá-la em prol do bem do nosso povo. Agradecemos à Universidade Federal de Viçosa, na pessoa do Magnífico Reitor, Prof. Dr. Demetrius David da Silva, que a 95 anos vem transformando a sociedade através de Ensino, Pesquisa e Extensão. Externamos também nossa gratidão ao Poder Executivo, na pessoa do Prefeito Municipal, Sr. Romário Batista Vieira, e Legislativo, na pessoa da Presidente da Câmara de Vereadores, Sr. Edson Márcio de Almeida, do município de Iúna-ES e a todos do staff administrativo que não mediram esforços para que este projeto fosse uma realidade. Não podemos nos esquecer do Dr. Jocsã Araújo, registrador de imóveis da comarca, um homem além do seu tempo e um entusiasta do tema direito de propriedade a todos. Registramos aqui nossos sinceros agradecimentos e reconhecimento do seu fundamental papel na realização deste projeto maior. Um agradecimento especial a toda equipe (professores, engenheiros, técnicos, contratados, estagiários) que lutou bravamente para que este projeto sobressaltasse barreiras, como por exemplo, COVID-19. Agradecemos ao Grupo de Pesquisa GeoTec, na pessoa do Prof. Dr. Gérson Rodrigues dos Santos, uma verdadeira família criada para gerar um conjunto de saberes para a transformação digital da gestão pública, além da formação técnica dos estudantes de Graduação, Mestrado, Doutorado e Pós-Doutorado da UFV. Não podemos esquecer do IPPDS – Instituto de Políticas Públicas e Desenvolvimento Sustentável, na pessoa do Diretor Prof. Dr. Marcelo José Braga e da servidora M.Sc. Karinne Galinari, responsáveis pela captação, apoio incondicional e direção do projeto. Finalmente, fica aqui externada nossa gratidão à toda equipe da Fundação FACEV da UFV, responsável pelo gerenciamento financeiro e prestação de contas do projeto, socorro sempre presente.
REFERÊNCIAS
ABNT, ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14653-1: Avaliação de bens – Parte 1: procedimentos gerais. Rio de Janeiro, 2001.
ABNT, ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 14563-2: Avaliaçãode bens – Parte 2: imóveis urbanos. Rio de Janeiro, 2010.
ALMEIDA, Carlos Augusto de, IBAPE – A Vistoria Do Imóvel Em Face Da Nova Norma Para Avaliação De Bens, NBR 14653
ANDRIOTTI, J.L.S. Fundamentos de Estatística e Geoestatística. Editora Unisino: São Leopoldo. 2013.
BAKER, P.T., Caudill S., Hodge, K. A., Talukder, D., Capano, C., Cornish, N.J., Multivariate classification with random forests for gravitational wave searches of black hole binary coalescence. Physical Review D, v.91, n. 6, 2014.
BREIMAN, L. Random forests. Machine learning, v. 45, n. 1, 2001, p. 5-32.
BRINK, H.; RICHARDS, J. W. Real-World Machine Learning. [s.n.], 2016.
CARVALHO, H. M. Aprendizado de máquina voltado para mineração de dados: árvores de decisão. Monografia (Graduação). Departamento de Engenharia de Software. Universidade de Brasília. Brasilia, 2014.
CHAVES, A. da C. F. Extração de Regras Fuzzy para Máquinas de Vetor Suporte (SVM) para Classificação em Múltiplas Classes. Tese (Doutorado). Programa de Pós-Graduação em Engenharia Elétrica da PUC-Rio. Rio de Janeiro. 2006.
COSENZA, D.N., LEITE, H.G., MARCATTI, G.E., BINOTI, D.H.B., ALCÂNTARA, A.E.M., RODE, R. Classificação da capacidade produtiva de sítios florestais utilizando máquina de vetor de suporte e rede neural artificial. Scientia Forestalis, Piracicaba, v. 43,n. 108, p. 955-963, 2015.
CRESSIE, N. Statistics for Spatial Data. Revised edn. New York, 1993.
DALAQUA, R.R., AMORIM, A., FLORES, E.F. Utilização de métodos combinados de avaliação imobiliária para a elaboração da planta de valores genéricos. Curitiba: Bol. Ciênc. Geod., sec. Artigos, Curitiba, v. 16, no 2, p.232-252, abr-jun, 2010.
LÁZARO, D. H. E. Aplicação de Máquinas de Vetores de Suporte na Identificação de Perfis de Alunos de acordo com Características da Teoria das Inteligências Múltiplas. Dissertação. o Programa de PósGraduação em Ciência da Computação. São José do Rio Preto 2016.
GIANNAKOS, I.B.S., LEÃO, M.L., Os Intervalos de Confiança e a Norma Brasileira - NBR 5676. IGEL -Instituto Gaúcho de Engenharia Legal e de Avaliações, VIII Ciclo de Estudos de Engenharia de Avaliações e Perícias, Porto Alegre, dezembro de 1996.
GIFFONI, F.deP., VILLELA, L.A. Estudos para a reforma tributária: tributação da renda e do patrimônio. Rio de Janeiro: Instituto de Pesquisas do IPEA. 77 p. 1987.
GUERRA, P. A. G. Geoestatística Operacional. Departamento Nacional da Produção Mineral, Brasília, 1988.
GUIA TURÍSTICO E COMERCIAL .Disponível em:.http://www.guiaturisticoecomerciales.com.br/. Acesso em set 2021.
HASTIE, T.; TIBSHIRANI, R.; FRIEDMAN, J. The elements of statistical learning. data mining, inference, and prediction. Second edition, New York: Springer series in statistics, 2009.739p
IBGE (Instituto Brasileiro de Geografia e Estatística). Censo Demográfico 2010. Disponível em: < https://censo2010.ibge.gov.br/>. Acesso em: set. 2021.
INCAPER (Instituto Capixaba de Pesquisa, Assistência Técnica e Extensão Rural). Programa de assistência técnica e extensão rural PROATER 2020 – 2023. Iúna, 2020.
ISAAKS, E. H.; SRIVASTAVA, M. An introduction to applied geostatistics. New York: Oxford University Press: 600 p. 1989.
JAMES, G; WITTEN, D; HASTIE, T; TIBSHIRANI, R. An Introduction to Statistical Learning with applications in R. Springer New York Heidelberg Dordrecht London, 2013.426p.
JOACHIMS, T. Learning to classify texts using support vector machines: methods, theory and algorithms. Kluwer Academic Publishers, 2002.
K. I. Kim, K. Jung, S. H. Park, and H. J. Kim. Support vector machines for texture classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, v.24, n.11, p.1542–1550, 2002.
LANDIM, P. M. B. Análise Estatística e dados geológicos. São Paulo: Fundação Editora da UNESP, 1998.
LIGAS, M., KULCZYCKI, M. Simple spatial prediction - least squares prediction, simple kriging, and conditional expectation of normal vector. Geodesy and Cartography, vol.59,n.2, p.69-81, 2010.
LOCH, C. A Realidade do cadastro técnico urbano no Brasil. Anais XIII Simpósio Brasileiro de Sensoriamento Remoto, Florianópolis, Brasil, 21-26 abril, INPE, p. 5357-5364,2007.
LORENA, A. C.; CARVALHO, A. C. Uma Introdução às Support Vector Machines. Revista de Informática Teórica e Aplicada, v. 14, n. 2, p. 43-67, 2007.
MELLO, J. M. DE; BATISTIA, J. L. F.; RIBEIRO JUNIOR, P. J.; OLIVEIRA, M. S. Ajuste e seleção de modelos espaciais de semivariograma visando à estimativa volumétrica de Eucaliptus grandis. Scientia Florestalis, v.1, n.69, p.25-37, 2005.
MENEZES, V.S.A. Algoritmo de classificação máquina de vetores suporte via suavização hiperbólica. Dissertação (Mestrado) Engenharia de Sistemas e Computação. Universidade Federal do Rio de Janeiro. 2007.
MITCHELL, T. M. Machine Learning. 1997.
MÖLLER, L.F.C. Planta de valores genéricos. 1. ed. Porto Alegre: Sagra-Luzzatto, 1995.
MOURA, E.M.; CARNEIRO, A.F.T. Planta de valores para municípios de pequeno porte: o caso de salgadinho – PE. Pernambuco, 2002.
MONARD, M.C.; BARANAUSKAS, J.A. Conceitos sobre Aprendizado de Máquina. Sistemas Inteligentes Fundamentos e Aplicações. 1ª ed. Barueri – SP: Manole Ltda, 2003. p. 89 – 114.
NADOLNY, M.L. A importância da planta genérica de valores na tributação municipal. Paraná: Revista Técnico-Científica do CREA-PR, 2016.
NOBLE, W.S. Support vector machine applications in computational biology. In B. Schölkopf, K. Tsuda, and J.-P. Vert, editors, Kernel Methods in computational biology, pages 71–92. MIT Press, 2004.
OLIVEIRA, A.A.F. Avaliação em massa com modelos de aprendizado de máquina aplicados aos terrenos urbanos do município de fortaleza, Dissertação(Mestre em Economia) - Programa de Economia Profissional, Universidade Federal do Ceará – UFC,Fortaleza-CE. 2020.
OSÓRIO, N.M.M., BRANDAIZE, M.C.B., ANTUNES, A.F.B. Uma metodologia para a estimação da perda de arrecadação do IPTU causada pela desatualização do cadastro imobiliário. Paraná: Revista Brasileira de Cartografia (2012) N0 64/2: 249-255, 2012.
PNUD (Programa das Nações Unidas para o Desenvolvimento). Ranking IDHM Municípios 2000. Brasil, 2000.
PONTIL, M.; VERRI, A. Support Vector Machines for 3-D Object Recognition. In IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.20, 1998, pp.637-646.
ROSA, L. M. F. Estudo sobre a influência de afirmações populares na Geoestatística Clássica. Tese (Doutorado). Departamento de Estatística da Universidade Federal de Viçosa. Viçosa,2017.
SANTOS, G. R.; OLIVEIRA, M. S.; LOUZADA, J. M.; SANTOS, A. M. R. T. Krigagem Simples versus Krigagem universal: qual o preditor mais preciso? Energia na Agricultura, v.26,n°2, p.49-55, 2011.
SANTOS, R.G., NASCIMENTO, S.P. A arrecadação do IPTU, no estado do paraná, no período de 1997 a 2011: um olhar sob os impactos da lei de responsabilidade fiscal. Curitiba: Revista Economia e Desenvolvimento, vol. 26, n. 1, 2014.
SANTOS, A. S. Geoestatística aplicada na avaliação da qualidade de dados 629 geoespaciais. Dissertação (Mestrado em Engenharia Civil)- Universidade Federal de Viçosa, Viçosa, MG, 148p., 2013.
SEPLAN (Secretaria de Estado do Planejamento). Zonas naturais do Espírito Santo: uma regionalização do estado, das microrregiões e dos municípios. Vitória, 1999.
SETUR (Secretaria de Estado de Turismo). Região das montanhas capixabas. Disponível em: < https://setur.es.gov.br/regiao-das-montanhas-capixabas >. Acesso em: set. 2021.
SMOLA, A. J., BARLETT, P., SCHOLKOPF, B., SCHUURMANS, D. (1999b). Introduction to Large Margin Classifiers, chapter 1, pages 1–28. InSmola et al. (1999a).
SUCHETANA, B., RAJAGOPALAN, B., SILVERSTEIN, J. Assessment of wastewater treatment facility compliance with decreasing ammonia discharge limits using a regression tree model. Science of The Total Environment, v. 598, p. 249-257, 2017.
VAPNIK, V. N. The Nature of Statistical Learning Theory. Springer-Verlag. 1995.
VIANA, R. S. M. O uso da geoestatística espaço-temporal e aprendizagem de máquina na predição da temperatura máxima do ar. Tese (Doutorado). Departamento de Estatística da Universidade Federal de Viçosa. Viçosa, 2019.
VIEIRA, C. A. O., SILVA, A. S., & MARCIANO, V. (2002). Automação do cadastro técnico municipal de cidades de pequeno porte. In Congresso Brasileiro de Cadastro Técnico Multifinalitário (Vol. 5, p. 12).
VIEIRA, S. R. Geoestatística em estudos de variabilidade espacial do solo. In: NOVAIS, R.F.;
ALVAREZ, V.H.; SCHAEFER, G.R. Tópicos em ciência do solo. Viçosa, v.1, p.1-54, 2000.
YAMAMOTO, J. K., LANDIM, P. M. B. Conceitos e Aplicações. Oficina de Textos: São Paulo, 2013. 216 p.
Este texto não substitui o Publicado no hall da Prefeitura Municipal de Iúna em 28/12/2021.
Este texto é meramente informativo e não exprime a orientação jurídica do órgão.